TensorFlow环境测试
创建两常数a和b,并生成一个会话Session,通过这个会话计算结果。
import tensorflow as tf
a = tf.constant([1.0,2.0],name="a")
b = tf.constant([2.0,3.0],name="b")
result = a + b
sess = tf.Session()
sess.run(result)
array([3., 5.], dtype=float32)
计算模型:计算图
计算图是TensorFlow中最基本的一个概念,TensorFlow中的所有计算都会被转换为计算图上的节点。
下面的代码产生了两个计算图,每个计算图定义了一个名字为v的变量,在计算图g1中,将v初始化为0;计算图g2中,将v初始化为1.可以看到当运行不同计算图时,变量v的值也是不一样的,TensorFlow中的计算图不仅可以用来隔离张量和计算,还提供了管理张量和计算的机制。
import tensorflow as tf
g1 = tf.Graph()
with g1.as_default():
#计算图g1中定义变量v,初始化为0
#v = tf.get_variable("v",initializer=tf.zeros_initializer(shape=[1]))
v=tf.get_variable("v",shape=[1],initializer=tf.zeros_initializer)
g2 = tf.Graph()
with g2.as_default():
#在计算图g2中定义变量v,并设置初始值为1
#v = tf.get_variable("v",initializer=tf.ones_initializer(shape=[1]))
v=tf.get_variable("v",shape=[1],initializer=tf.ones_initializer)
#在计算图g1中读取v的取值
with tf.Session(graph=g1) as sess:
#tf.initialize_all_variables().run()
tf.global_variables_initializer().run()
with tf.variable_scope("",reuse=True):
#在计算图g1中,变量v的取值应该为0,下面输出[0.]
print(sess.run(tf.get_variable("v")))
#在计算图g2中读取v的取值
with tf.Session(graph=g2) as sess:
#tf.initialize_all_variables().run()
tf.global_variables_initializer().run()
with tf.variable_scope("",reuse=True):
#在计算图g2中,变量V的取值为1,下面输出[1.]
print(sess.run(tf.get_variable("v")))
[0.]
[1.]
数据模型:张量
张量,即Tensor。零阶张量为标量,一阶张量为向量,二阶张量为一维数组,n阶张量为n维数组。在张量中并没有真正保存数字,它保存的是如何得到这些数字的计算过程,输出一个张量的结构。一个张量主要保存三个属性:名字(name)、维度(shape)和类型(type)。
import tensorflow as tf
a = tf.constant([1.0,2.0],name="a")
b = tf.constant([2.0,3.0],name="b")
result = tf.add(a,b,name="add")
print(result)
Tensor("add_6:0", shape=(2,), dtype=float32)
运行模型:会话
利用会话session来执行定义好的运算。
#创建一个会话
sess = tf.Session()
#使用这个创建好的会话来运行结果
sess.run(...)
#关闭会话
sess.close()
with tf.Session() as sess:
#使用这创建的会话来计算关心的结果
sess.run(...)
#不需要close。。。。。。。。。。
设置默认对话窗口计算张量的取值:
sess = tf.Session()
with sess.as_default():
print(result.eval())
将生成的会话注册为默认会话:
sess = tf.InteractiveSession()
print(result.eval())
sess.close()
[3. 5.]
神经网络的实现
TensorFlow游乐场
TensorFlow游乐场是一个通过网页浏览器就可以实现训练的简单神经网络,并实现可视化训练过程的工具。其页面左侧提供了4种不同的数据集来测试神经网络。默认的数据为左上角被框出来的那个。被选中数据会显示在右边的输出里。
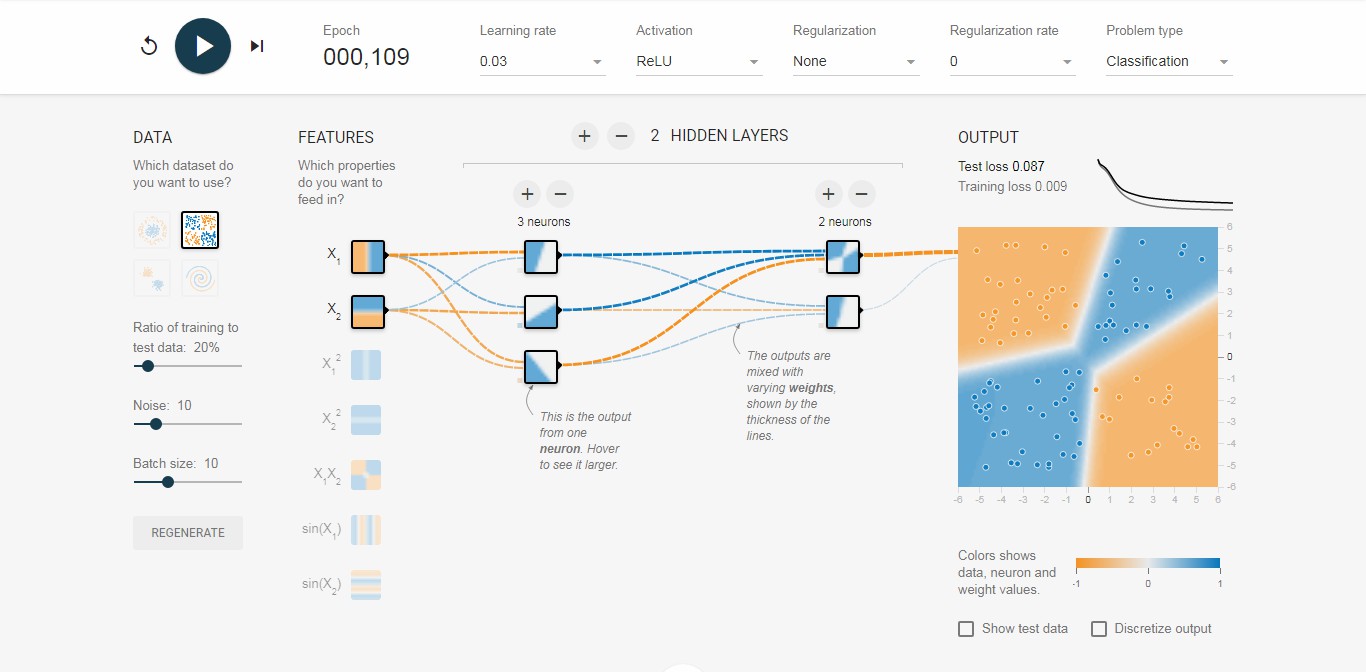
比如某工厂的零件,用长度和质量两个特征描述,被分为合格和不合格两类。网络第一层为输入层,用于输入特征向量;第二层为隐藏层,一般隐藏层越多,网络越深,即深度网络,可以增加或减少。游乐场还支持选择网络每一层的节点数、学习率、激活函数、正则化。
其中激活函数有:ReLU、Tanh、Sigmoid、Linear等,对分类结果及收敛时间影响不同。ReLU对非线性分类收敛快,效果好。
-
提取特征向量
-
定义神经网络结构
-
调整参数
-
使用网络预测未知数据
变量初始化
#正态分布随机初始化
#seed随机种子保证每次运行的结果是一样的
weights = tf.Variable(tf.random_normal([2,3],stddev=2,seed=1))
#全零初始化
biases = tf.Variable(tf.zeros([3]))
#w2设置为weights的值
w2 = tf.Variable(weights.initialized_value())
#w3设置为weights的两倍
w3 = tf.Variable(weights.initialized_value() * 2.0)
前向传播
import tensorflow as tf
w1 = tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2 = tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
x = tf.constant([[0.7,0.9]])
a = tf.matmul(x,w1)#矩阵相乘
y = tf.matmul(a,w2)
sess = tf.Session()
#将w1,w2初始化
#sess.run(w1.initializer)
#sess.run(w2.initializer)
#print(sess.run(y))
#sess.close()
#便捷的方式,多变量时简便
init_op = tf.initialize_all_variables()
sess.run(init_op)
sess.run(y)
array([[3.957578]], dtype=float32)
#通过placeholder实现前向传播
import tensorflow as tf
w1 = tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2 = tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
x = tf.placeholder(tf.float32,shape=(1,2),name="input")
a = tf.matmul(x,w1)
y = tf.matmul(a,w2)
sess = tf.Session()
init_op = tf.initialize_all_variables()
sess.run(init_op)
#一个样例的前向传播结果
print(sess.run(y,feed_dict={x:[[0.7,0.9]]}))
[[3.957578]]
#通过placeholder实现前向传播
import tensorflow as tf
w1 = tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2 = tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
#3个样例的前向传播结果
x = tf.placeholder(tf.float32,shape=(3,2),name="input")
a = tf.matmul(x,w1)
y = tf.matmul(a,w2)
sess = tf.Session()
init_op = tf.initialize_all_variables()
sess.run(init_op)
#3个样例的前向传播结果
print(sess.run(y,feed_dict={x:[[0.7,0.9],[0.1,0.4],[0.5,0.8]]}))
[[3.957578 ]
[1.1537654]
[3.1674924]]
解决二分类问题
-
定义神经网络的结构和前向传播的输出结果
-
定义损失函数以及选择反向传播优化的算法
-
生成会话并且在训练数据上反复运行反向传播优化算法
import tensorflow as tf
from numpy.random import RandomState
#定义训练数据batch的大小
batch_size = 8;
#定义神经网络参数
w1 = tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2 = tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
x = tf.placeholder(tf.float32,shape=(None,2),name='x-input')
y_ = tf.placeholder(tf.float32,shape=(None,1),name='y-input')
a = tf.matmul(x,w1)
y = tf.matmul(a,w2)
#定义损失函数和反向传播的算法
cross_entropy = -tf.reduce_mean(
y_*tf.log(tf.clip_by_value(y,1e-10,1.0)))
train_step = tf.train.AdamOptimizer(0.001).minimize(cross_entropy)
#通过随机数生成一个模拟数据集
rdm = RandomState(1)
dataset_size = 128
X = rdm.rand(dataset_size,2)
#定义规则来给出样本的标签,在这里所有的x1+x2<1的洋烈都被认为是正样本(合格)
#0表示负样本,1表示正样本
Y = [[int(x1+x2<1)] for (x1,x2) in X]
with tf.Session() as sess:
init_op = tf.initialize_all_variables()
#初始化变量
sess.run(init_op)
print("w1:",sess.run(w1))
print("w2:",sess.run(w2))
#设定训练论数
steps = 5000
for i in range(steps):
#每次选取batch_size个样本训练
start = (i*batch_size) % dataset_size
end = min(start+batch_size,dataset_size)
#通过选取的样本训练神经网络并更新参数
sess.run(train_step,
feed_dict={x:X[start:end],y_:Y[start:end]})
if i % 1000 == 0:
#每隔一段时间计算在所有数据上的交叉熵
total_cross_entropy = sess.run(
cross_entropy,feed_dict={x:X,y_:Y})
print("After %d training step(s),cross entropy on all data is %g" % (i,total_cross_entropy))
#随着训练的进行,交叉熵是逐渐变小的
#交叉熵越小说明越策的结果越真实的结果差距越小
print("w1:",sess.run(w1))
print("w2:",sess.run(w2))
#可以发现这两个参数的取值已经发生变化
#这个变化的就是训练的结果
#它使得这个神经网络能更好的拟合数据
w1: [[-0.8113182 1.4845988 0.06532937]
[-2.4427042 0.0992484 0.5912243 ]]
w2: [[-0.8113182 ]
[ 1.4845988 ]
[ 0.06532937]]
After 0 training step(s),cross entropy on all data is 0.0674925
After 1000 training step(s),cross entropy on all data is 0.0163385
After 2000 training step(s),cross entropy on all data is 0.00907547
After 3000 training step(s),cross entropy on all data is 0.00714436
After 4000 training step(s),cross entropy on all data is 0.00578471
w1: [[-1.9618274 2.582354 1.6820377]
[-3.4681718 1.0698233 2.11789 ]]
w2: [[-1.8247149]
[ 2.6854665]
[ 1.418195 ]]
深层神经网络
这里将进一步介绍如何设计和优化神经网络,使得它能够更好地对未知的样本进行预测。
线性模型的局限性
在线性模型中,模型的输出为输入的加权和。假设一个模型的输出y和输入xi满足以下关系,那么这个模型就是一个线性模型:$y=\sum {w_i} {x_i} +b$.
前向传播的公式为:$a^{(1)}=xW^{(1)},y=a^{(1)}W^{(2)}$
输出为:$y=(xW^{(1)})W^{(2)}$
因为线性模型的组合仍是线性模型,所以前向传播符合线性模型的定义,然而线性模型解决问题的能力是有限的。
激活函数实现去线性化
如果神经网络的输出为所有输入的加权和,则导致神经网络是一个非线性函数,那么整个神经网络的模型也就不再是线性的了。这个非线性函数就是激活函数。输出为:$f(\sum{x_i}{w_i}+b)$.
ReLU函数:$f(x)=max(x,0)$
sigmoid函数:$f(x)=\frac{1}{1+e^{-x}}$
tanh函数:$f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$
前向传播的实现:
a = tf.nn.relu(tf.matmul(x,w1)+biases1)
y = tf.mm.relu(tf.matmul(a,w2)+biases2)
损失函数
分类问题
-
交叉熵:$H(p,q)=-\sum{p(x)}{\log{q(x)}}$,如下实现交叉熵,y_代表正确结果,y代表预测结果,tf.clip_by_value可以避免类似log0的错误运算:
cross_entropy = -tf.reduce_mean( y_*tf.log(tf.clip_by_value(y,1e-10,1.0)))
-
softmax回归:$softmax(y_i)=y^{‘}{i}=\frac{e^{yi}}{\sum^{n}{j=1}e^{yj}}$,这样就把一个神经网络的输出变成了一个概率分布,从而可以通过
交叉熵来计算预测的概率分布和真实分布之间的距离了。cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y,y_)
回归问题
与分类问题不同,回归问题解决的是对具体数值的预测,比如房价预测,销量预测等。这些问题需要预测不是一个实现定义好的类别,而是一个任意实数。解决回归问题的神经网络一般只有一个输出节点,这个节点的输出值就是预测值。对于回归问题,最常用的损失函数就是均方误差MSE:$MSE(y,y^{‘})=\frac{\sum{(y_i-y^{‘}_{i}})^2}{n}$
其中$y_i$为正确答案,$y^{‘}_{i}$为神经网络给出的预测值,实现代码为:
mse = tf.reduce_mean(tf.square(y_-y))
自定义损失函数
tf.greater输入两张量,第一个参数为选择依据,选择条件true时输出第二个参数中的值,否则输出第三参数。
loss = tf.reduce_sum(tf.select(tf.greater(v1,v2),
(v1-v2)*a,(v2-v1)*b))
新版本中,tf.select()被改为tf.where()
#带有损失函数的神经网络
import tensorflow as tf
from numpy.random import RandomState
batch_size = 8
#两个输入节点
x = tf.placeholder(tf.float32,shape=(None,2),name='x-input')
#回归问题一般只有一个输出节点
y_ = tf.placeholder(tf.float32,shape=(None,1),name='y-input')
#定义一个单层的神经网络前向传播的过程,这就是简单加权和
w1 = tf.Variable(tf.random_normal([2,1],stddev=1,seed=1))
y = tf.matmul(x,w1)
#定义预测多了和预测少了的成本
loss_less = 10
loss_more = 1
loss = tf.reduce_sum(tf.where(tf.greater(y,y_),
(y-y_)*loss_more,
(y_-y)*loss_less))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
#通过随机数生成一个模拟数据集
rdm = RandomState(1)
dataset_size = 128
X = rdm.rand(dataset_size,2)
#设置回归正确值为两个输入的和加上一个随机量,即噪声
#噪声为-0.05~0,05的随机数
Y = [[x1+x2+rdm.rand()/10.0-0.05] for (x1,x2) in X]
#训练神经网络
with tf.Session() as sess:
init_op = tf.initialize_all_variables()
sess.run(init_op)
steps = 5000
for i in range(steps):
start = (i*batch_size)%dataset_size
end = min(start+batch_size,dataset_size)
sess.run(train_step,feed_dict={x:X[start:end],y_:Y[start:end]})
#print(sess.run(w1))
#得到w1值为[1.01934695,1.04280889]
神经网络优化算法
-
先通过前向传播计算预测值,并将预测值和真实值做对比得出两者之间的差距
-
再通过反向传播算法计算损失函数对每一个参数的梯度
-
再根据梯度和学习率更新参数
这里将更加具体地介绍如何通过反向传播算法和梯度下降算法调整神经网络中参数的取值。梯度下降算法主要用于优化单个参数的取值,而反向传播算法给出了一个高效的方式在所有参数上使用梯度下降算法,从而使神经网络模型在训练数据上的损失函数尽可能小。反向传播算法是训练神经网络的核心算法,它可以根据定义好的损失函数优化神经网络中参数的取值,从而使神经网络模型在训练数据集上的损失函数达到一个较小值。
假设用$\theta$表示神经网络中的参数,$J(\theta)$表示在给定的参数取值下,训练数据集上损失函数的大小,那么整个优化过程可以抽象为寻找一个参数$\theta$,使得$J(\theta)$最小。因为目前没有一个通用的方法可以对任意损失函数直接求解最佳的参数取值,所以在实践中,梯度下降算法是最常用的神经网络优化方法。
参数更新的公式:$\theta_{n+1}=\theta_{n}-\eta \frac{\partial}{\partial \theta_{n}}J(\theta_{n})$
使用梯度下降算法优化$J(x)=x^2$
| 轮数 | 当前值 | 梯度x学习率 | 更新参数值 |
|---|---|---|---|
| 1 | 5 | 2x5x0.3=3 | 5-3=2 |
| 2 | 2 | 2x2x0.3=1.2 | 2-1.2=0.8 |
| 3 | 0.8 | 2x0.8x0.3=0.48 | 0.8-0.48=0.32 |
| 4 | 0.32 | 2x0.32x0.3=0.192 | 0.32-0.192=0.128 |
| 5 | 0.128 | 2x0.128x0.3=0.0768 | 0.128-0.0768=0.0512 |
经过5次迭代后,参数x的值变成了0.0512,这个和参数最优值0已经比较接近了。
需要注意的是,梯度下降算法并不能保证被优化的函数能到达全局最优解,只有当损失函数为凸函数时,梯度下降算法才能保证达到全局最优解。梯度下降算法另外一个问题是耗时。为了综合梯度下降算法和随机梯度下降算法的优缺点,在实际应用中一般采用这两个算法的折中,每次计算一小部分训练数据的损失函数。这一小部分数据被称之为一个batch。通过矩阵运算,每次在一个batch上优化神经网络的参数并不会比单个数据慢太多。另外,每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果。
本文中神经网络训练大致遵循以下过程:
batch_size = n
#每次取一小部分数据
x = tf.placeholder(tf.float32,shape=(batch_size,2),name='x-input')
y_ = tf.placeholder(tf.float32,shape=(batch_size,1),name='y-input')
#定义神经网络结构和优化算法
loss = ...
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
#训练神经网络
with tf.Session() as sess:
#参数初始化
...
#更新参数
for i in range(steps):
#准备batch_size个训练数据
#一般将所有数据随机打乱再选取
current_X,current_Y = ...
sess.run(train_step,feed_dict={x:current_X,y_:current_Y})
进一步优化
学习率指数衰减
通过指数衰减的学习率即可以让模型在训练的前期快速接近较优解,又可以保证模型在训练后期不会有太大的波动,从而更加接近局部最优。decayed_learning_rate为每一轮优化时使用的学习率,learning为事先设定的初始学习率,decay_rate为衰减系数,decay_steps为衰减速度。初始学习率为0.1,没训练100学习率乘以0.96,。
global_step = tf.Variable(0)
#生成学习率
learning_rate = tf.train.exponential_decay(
0.1,global_step,100,0.96,staircase=True)
#使用指数衰减的学习率
learning_step = tf.train.GradientDescentOptimizer(learning_rate)\
.minimize(..my loss...,global_step=global_step)
decayed_learning_rate = \
learning_rate * decay_rate^(global_step/decay_steps)
正则化避免过拟合
为了避免过拟合问题,一个常用的方法是正则化,即在损失函数中加入刻画模型复杂程度的指标,$J(\theta)+\lambda R(w)$。L1正则化$R(w)=\sum w_i$。L2正则化$R(w)=\sum w^{2}_i$.无论哪种正则化方式,基本思想都是希望通过限制权重的大小,使得模型不能任意拟合数据中的随机噪声。其中L1正则化会让参数变得更加稀疏(参数变为0),L2不会。其次,L1不可导,L2可导,对含有L2正则化损失函数的优化更加简洁。
w = tf.Variable(tf.random_normal([2,1],stddev=1,seed=1))
y = tf.matmul(x,w)
loss = tf.reduce_mean(tf.square(y_-y))
+tf.contrib.layers.l2_regularizer(lambda)(w)
import tensorflow as tf
#获取一层神经网络上的权重,并将权重的L2正则化损失加入名为losses的集合中
def get_weight(shape,lambda):
#生成一个变量
var = tf.Variable(tf.random_normal(shape),dtype=tf.float32)
#add_to_collection函数将这个新生成变量的L2正则化损失项加入集合
#这个函数的第一个参数losses是集合的名字,第二个是要加入这个集合的内容
tf.add_to_collection(
'losses',tf.contrib.layers.l2_regularizer(lambda)(var))
#返回生成的变量
return var
x = tf.placeholder(tf.float32,shape=(None,2))
y_ = tf.placeholder(tf.float32,shape=(None,1))
batch_size=8;
#定义每一层网络中节点的个数
layer_dimension=[2,10,10,10,1]
#神经网络的层数
n_layers=len(layer_dimension)
#这个变量维护前向传播时最深层的节点,开始的时候就是输入层
cur_layer=x
#当前层的节点个数
in_dimension=layer_dimension[0]
#通过一个循环来生成5层全连接的神经网络结构
for i in range(1,n_layers):
#layer_dimension[i]为下一层节点个数
out_dimension=layer_dimension[i]
#生成当前层中权重的变量,并将这个变量的L2正则化损失加入计算图集合
weight=get_weight([in_dimension,out_dimension],0.001)
bias=tf.Variable(tf.constant(0.1,shape=[out_dimension]))
#使用ReLU激活函数
cur_layer=tf.nn.relu(tf,matmul(cur_layer,weight)+bias)
#进入下一层之前将下一层的节点个数更新为当前节点个数
in_dimension=layer_dimension[i]
#在定义神经网络前向传播的同时已经将所有的L2正则化损失加入到了图上的集合
#这里只需要计算刻画模型在训练数据上表现的损失函数
mse_loss=tf.reduce_mean(tf.square(y_-cur_layer))
#将均方误差损失函数加入损失集合
tf.add_to_collection('losses',mse_loss)
#get_collection返回一个列表
#把所有损失函数部分相加得到最终损失函数
loss=tf.add_n(tf.get_collection('losses'))
滑动平均模型会将每一轮迭代得到的模型综合起来,从而使得最终的模型更加鲁棒。
shadow_variable = decay x shadow_variable+(1-decay)xvariable
shadow_variable为影子变量,variable为待更新的变量,decay为衰减率。如果提供了num_updates参数,则衰减率为$min(decay,\frac{1+num_updates}{10+num_updates})$,通过ExponentialMovingAverage实现滑动平均:
import tensorflow as tf
#定义一个变量用于计算滑动平均,这个变量的初始值为0
v1 = tf.Variable(0,dtype=tf.float32)
#这里的step变量模拟神经网络中迭代的轮数,用于控制衰减率
step = tf.Variable(0,trainable=False)
#定义一个滑动平均的类,初始化给定衰减率0.99和step
ema = tf.train.ExponentialMovingAverage(0.99,step)
#定义一个更新变量滑动平均的操作,给定一个列表,每次执行操作时列表都会更新
maintain_averages_op = ema.apply([v1])
with tf.Session() as sess:
#初始化变量
init_op = tf.initialize_all_variables()
sess.run(init_op)
#通过ema.average(v1)获取滑动平均之后变量的取值
#在初始化之后变量v1的值和v1的滑动平均都为0
print(sess.run([v1,ema.average(v1)]))
#输出[0.0,0.0]
#更新变量v1的值到5
sess.run(tf.assign(v1,5))
#更新v1的滑动平均值
#衰减率为min{0.99,(1+step)/(10+step)=0.1}=0.1
#所以v1的滑动平均会被更新为0.1x0+0.9x5=4.5
sess.run(maintain_averages_op)
print(sess.run([v1,ema.average(v1)]))
#输出[5.0,4.5]
#更新step值为10000
sess.run(tf.assign(step,10000))
#更新v1的值为10
sess.run(tf.assign(v1,10))
#更新v1的滑动平均
#衰减率为min{0.99,(1+step)/(10+step)=0.1}=0.99
#所以v1的滑动平均会被更新为0.99x4.5+0.01x10=4.555
sess.run(maintain_averages_op)
print(sess.run([v1,ema.average(v1)]))
#输出[10.0,4.5549998]
#再次更新滑动平均平均值
#得到的新滑动平均值为0.99x4.555+0.01x10=4.60945
sess.run(maintain_averages_op)
print(sess.run([v1,ema.average(v1)]))
#输出[10.0,4.6094499]
[0.0, 0.0]
[5.0, 4.5]
[10.0, 4.555]
[10.0, 4.60945]
数字识别问题
将训练和测试分为两个独立的程序,这可以使得每一个组件更加灵活。比如训练神经网络的程序可以持续输出训练好的模型,而测试程序可以每隔一段时间检验最新模型的正确率,如果模型效果好,则将这个模型提供给产品使用。
将前向传播的过程抽象成一个单独的库函数,因为神经网络的前向传播过程在训练和测试的过程中都会用到,所以通过库函数的方式使用起来既可以更加方便,又可以保证训练和测试过程中使用的前向传播方法一定是一致的。
-
mnist_inference.py:定义了前向传播的过程以及神经网络的参数
-
mnist_train.py:定义了神经网络的训练过程
-
mnist_eval.py:定义了测试过程
mnist_inference.py
#-*- coding:utf-8 -*-
import tensorflow as tf
#定义神经网络相关参数
input_node = 784
output_node = 10
layer1_node = 500
def get_weight_variable(shape,regularizer):
weights = tf.get_variable(
"weights",shape,
initializer=tf.truncated_normal_initializer(stddev=0.1))
#将张量加入集合
if regularizer != None:
tf.add_to_collection('losses',regularizer(weights))
return weights
#定义神经网络前向传播
def inference(input_tensor,regularizer):
#声明第一层网络变量
with tf.variable_scope('layer1'):
weights = get_weight_variable(
[input_node,layer1_node],regularizer)
biases = tf.get_variable(
"biases",[layer1_node],
initializer = tf.constant_initializer(0.0))
layer1 = tf.nn.relu(tf.matmul(input_tensor,weights)+biases)
#声明第二层变量
with tf.variable_scope('layer2'):
weights = get_weight_variable(
[layer1_node,output_node],regularizer)
biases = tf.get_variable(
"biases",[output_node],
initializer=tf.constant_initializer(0.0))
layer2 = tf.matmul(layer1,weights)+biases
#返回前向传播的结果
return layer2
mnist_train.py
#-*- coding:utf-8 -*-
import os
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#加载mnist_inference.py中定义的常量和前向传播的函数
import mnist_inference
#配置神经网络的参数
batch_size = 100
learning_rate_base = 0.8
learning_rate_decay = 0.99
regularaztion_rate = 0.0001
training_steps = 30000
moving_average_decay = 0.99
#模型保存的路径和文件名
model_save_path = "/path/to/model"
model_name = "model.ckpt"
def train(mnist):
#定义输入输出placeholder
x = tf.placeholder(
tf.float32,[None,mnist_inference.input_node],name='x-input')
y_ = tf.placeholder(
tf.float32,[None,mnist_inference.output_node],name='y-input')
regularizer = tf.contrib.layers.l2_regularizer(regularaztion_rate)
#使用前向传播
y = mnist_inference.inference(x,regularizer)
global_step = tf.Variable(0,trainable=False)
#定义损失函数、学习率、滑动平均操作以及训练过程
variable_averages = tf.train.ExponentialMovingAverage(
moving_average_decay,global_step)
variables_averages_op = variable_averages.apply(
tf.trainable_variables())
#cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(y,tf.argmax(y_,1))
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_,1))
cross_entropy_mean = tf.reduce_mean(cross_entropy)
loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
learning_rate = tf.train.exponential_decay(
learning_rate_base,
global_step,
mnist.train.num_examples / batch_size,
learning_rate_decay)
train_step = tf.train.GradientDescentOptimizer(learning_rate)\
.minimize(loss,global_step=global_step)
with tf.control_dependencies([train_step,variables_averages_op]):
train_op = tf.no_op(name='train')
#初始化TensorFlow持久类
saver = tf.train.Saver()
with tf.Session() as sess:
tf.initialize_all_variables().run()
#在训练过程中不再测试模型在验证数据上的表现
#验证和测试的过程将会有一个独立的程序
for i in range(training_steps):
xs,ys = mnist.train.next_batch(batch_size)
_,loss_value,step = sess.run([train_op,loss,global_step],
feed_dict={x:xs,y_:ys})
#每1000轮保存一次模型
if i % 1000 == 0:
#输出当前训练情况
print("after %d training step(s),loss on training"
"batch is %g." % (step,loss_value))
saver.save(
sess,os.path.join(model_save_path,model_name),
global_step=global_step)
#saver中max_to_keep属性为5
#第6次保存删掉第1次保存
#第7次保存删掉第2次保存
def main(argv=None):
mnist = input_data.read_data_sets("/tmp/data",one_hot=True)
train(mnist)
if __name__ == '__main__':
tf.app.run()
mnist_eval.py
# -*- coding:utf-8 -*-
#####################################
#程序每隔10秒运行一次
#每次运行都是读取最新保存的模型
#并在验证数据集上计算模型的正确率
#####################################
import time
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#加载mnist_inference.py和mnist_train.py中定义的常数和函数
import mnist_inference
import mnist_train
#每10秒加载一次最新的模型,并在测试数据上测试最新模型的正确率
eval_interval_secs = 10
def evaluate(mnist):
with tf.Graph().as_default() as g:
#定义输入输出的格式
x = tf.placeholder(
tf.float32,[None,mnist_inference.input_node],name='x-input')
y_ = tf.placeholder(
tf.float32,[None,mnist_inference.output_node],name='y-input')
validate_feed = {x:mnist.validation.images,
y_:mnist.validation.labels}
#计算前向传播结果
#因为测试不关注正则化损失
#所以用于计算正则化损失的函数被设置为None
y = mnist_inference.inference(x,None)
#使用前向传播的结果计算正确率
#如果需要对未知的样例进行分类
#那么使用tf.argmax(y,1)就可以得到输入样例的预测类别了
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
#通过变量重命名的方式加载模型
#这样在前向传播的过程中就不需要调用求滑动平均的函数来求平均值
variable_averages = tf.train.ExponentialMovingAverage(
mnist_train.moving_average_decay)
variables_to_restore = variable_averages.variables_to_restore()
saver = tf.train.Saver(variables_to_restore)
#每隔eval_interval_secs秒调用一次计算正确率的过程以检测训练过程中正确率变化
while True:
with tf.Session() as sess:
#tf.train.get_checkpoint_state函数会通过checkpoint文件自动找到目录中最新模型的文件名
ckpt = tf.train.get_checkpoint_state(
mnist_train.model_save_path)
if ckpt and ckpt.model_checkpoint_path:
#加载模型
saver.restore(sess,ckpt.model_checkpoint_path)
#通过文件名得到模型保存时迭代的轮数
global_step = ckpt.model_checkpoint_path\
.split('/')[-1].split('-')[-1]
accuracy_score = sess.run(accuracy,
feed_dict=validate_feed)
print("after %s training step(s),validation "
"accuracy = %g" % (global_step,accuracy_score))
else:
print('No checkpoint file found')
return
time.sleep(eval_interval_secs)
def main(argv=None):
mnist = input_data.read_data_sets("/tmp/data",one_hot=True)
evaluate(mnist)
if __name__ == '__main__':
tf.app.run()