程序返回一个 5x5 的单位矩阵
A = [[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1]]
A = np.eye(5)
然后绘制给定数据x与y的图像
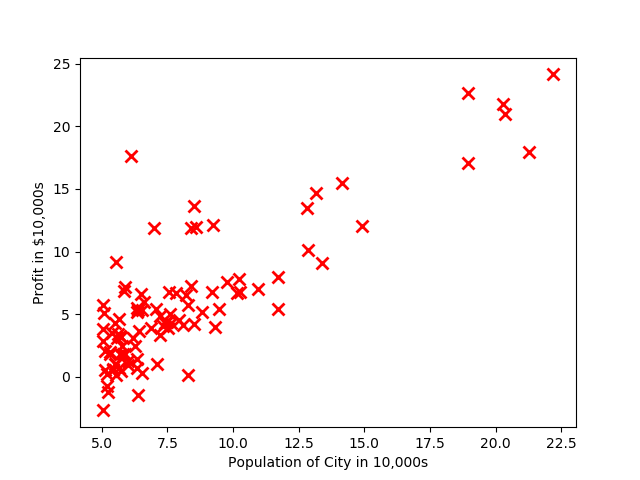
计算线性回归的代价
前面有系数2的原因是下面求梯度是对每个变量求偏导,2可以消去
注意这里的X是真实数据前加了一列1,因为有theta(0)
梯度下降算法学习参数theta
代价函数对 $\theta_{j}$ 求偏导:
theta更新为:
$\alpha$ 为学习速率,控制梯度下降的速度,一般取0.01,0.03,0.1,0.3…..
打印theta[0], theta[1]:-3.630291,1.166362
在绘制数据点的基础上绘制回归得到直线
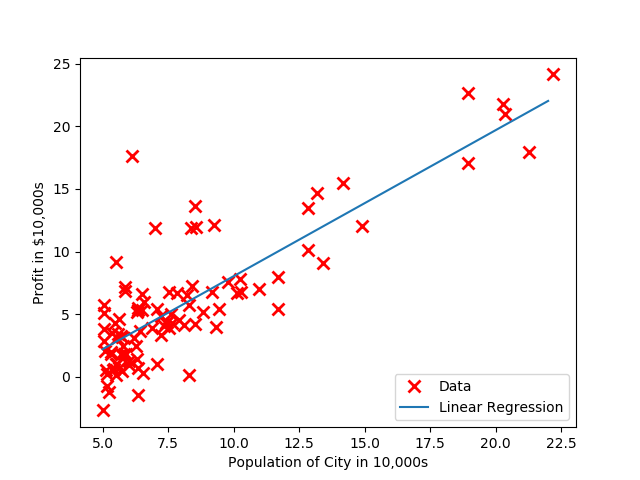
可视化代价函数
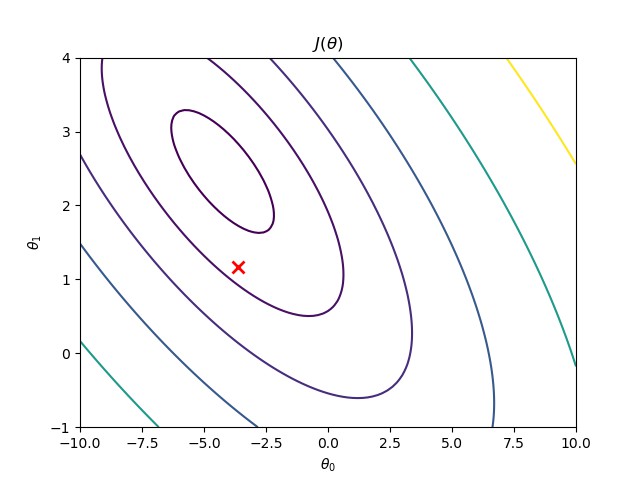
本文涉及到的数据集:PRML_LR_data.txt
程序代码
# coding: utf-8
# If you use python 2, uncomment the following line.
# from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
def warm_up_exercise():
"""热身练习"""
A = None
# ====================== 你的代码 ==========================
# 在下面加入你的代码,使程序返回一个 5x5 的单位矩阵
A = [[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1]]
# =========================================================
return A
def plot_data(x, y):
"""绘制给定数据x与y的图像"""
plt.figure()
# ====================== 你的代码 ==========================
# 绘制x与y的图像
# 使用 matplotlib.pyplt 的命令 plot, xlabel, ylabel 等。
# 提示:可以使用 'rx' 选项使数据点显示为红色的 "x",
# 使用 "markersize=8, markeredgewidth=2" 使标记更大
# 给制数据
plt.plot(x, y, 'rx', markersize=8, markeredgewidth=2)#or圆点
# 设置y轴标题为 'Profit in $10,000s'
plt.ylabel('Profit in $10,000s')
# 设置x轴标题为 'Population of City in 10,000s'
plt.xlabel('Population of City in 10,000s')
# =========================================================
plt.show()
def compute_cost(X, y, theta):
"""计算线性回归的代价"""
m = len(y)
J = 0.0
# ====================== 你的代码 ==========================
# 计算给定 theta 参数下线性回归的代价
# 请将正确的代价赋值给 J
# 注意:在主函数中将行向量变列向量
J = (1.0/(2*m))*np.sum(np.square(X.dot(theta)-y))
# J = (np.transpose(X*theta-y))*(X*theta-y)/(2*m) #计算代价J
# =========================================================
return J
def gradient_descent(X, y, theta, alpha, num_iters):
"""执行梯度下降算法来学习参数 theta"""
m = len(y)
J_history = np.zeros((num_iters,))
for iter in range(num_iters):
# ====================== 你的代码 ==========================
# 计算给定 theta 参数下线性回归的梯度,实现梯度下降算法
deltaTheta = (1.0/m)*(X.T.dot(X.dot(theta)-y))
# =========================================================
# 将各次迭代后的代价进行记录
J_history[iter] = compute_cost(X, y, theta)
theta = theta-alpha*deltaTheta
# ==========================================================
return theta, J_history
def plot_linear_fit(X, theta):
"""在绘制数据点的基础上绘制回归得到直线"""
# ====================== 你的代码 ==========================
# 绘制x与y的图像
# 使用 matplotlib.pyplt 的命令 plot, xlabel, ylabel 等。
# 提示:可以使用 'rx' 选项使数据点显示为红色的 "x",
# 使用 "markersize=8, markeredgewidth=2" 使标记更大
# 使用"label=<your label>"设置数据标识,
# 如 "label='Data'" 表示原始数据点
# "label='Linear Regression'" 表示线性回归的结果
# 绘制数据
xx = np.arange(5,23)
yy = theta[0]+xx*theta[1]
plt.plot(X[:,1], y, 'rx', label='Data', markersize=8, markeredgewidth=2)
plt.plot(xx,yy,label='Linear Regression')
# 使用 legned 命令显示图例,图例显示位置为 "loc='lower right'"
plt.legend(loc='lower right')
# 设置y轴标题为 'Profit in $10,000s'
plt.ylabel('Profit in $10,000s')
# 设置x轴标题为 'Population of City in 10,000s'
plt.xlabel('Population of City in 10,000s')
# =========================================================
plt.show()
def plot_visualize_cost(X, y, theta_best):
"""可视化代价函数"""
# 生成参数网格
theta0_vals = np.linspace(-10, 10, 101)
theta1_vals = np.linspace(-1, 4, 101)
t = np.zeros((2, 1))
J_vals = np.zeros((101, 101))
for i in range(101):
for j in range(101):
# =============== 你的代码 ===================
# 加入代码,计算 J_vals 的值
J_vals[i,j] = (1.0/(2*len(y)))*np.sum(np.square(theta0_vals[i]+X.dot(theta1_vals[j])-y))
# pass # 完成你的代码后请删除此行
# ===========================================
'''
# 二维曲线
X=X[:,1]
#theta2=np.arange(-10,11,0.01)
theta2=np.linspace(-10,11,101)
n=y.size
J=np.zeros(theta2.size)
for i in np.arange(theta2.size):
J[i]=(1.0/(2*n))*np.sum(np.square(X.dot(theta2[i])-y))
plt.plot(theta2, J)
'''
# 绘制等高线
plt.figure()
plt.contour(theta0_vals, theta1_vals, J_vals,
levels=np.logspace(-2, 3, 21))
plt.plot(theta_best[0], theta_best[1], 'rx',
markersize=8, markeredgewidth=2)
plt.xlabel(r'$\theta_0$')
plt.ylabel(r'$\theta_1$')
plt.title(r'$J(\theta)$')
plt.show()
if __name__ == '__main__':
print('Running warm-up exercise ... \n')
print('5x5 Identity Matrix: \n')
A = warm_up_exercise()
print(A)
print('Plotting Data ...\n')
data = np.loadtxt('PRML_LR_data.txt', delimiter=',')
x, y = data[:, 0], data[:, 1]
m = len(y)
plot_data(x, y)
plt.show()
print('Running Gradient Descent ...\n')
# Add a column of ones to x
X = np.ones((m, 2))
X[:, 1] = data[:, 0]
# 将行向量转换为列向量
# X = np.c_[np.ones(data.shape[0]), data[:,0]]
# y = np.c_[data[:, 1]]
X = np.c_[X]
y = np.c_[y]
# initialize fitting parameters
theta = np.zeros((2, 1))
# Some gradient descent settings
iterations = 1500
alpha = 0.01
# compute and display initial cost
# Expected value 32.07
J0 = compute_cost(X, y, theta)
print(J0)
# run gradient descent
# Expected value: theta = [-3.630291, 1.166362]
theta, J_history = gradient_descent(X, y,theta, alpha,iterations)
print('Theta found by gradient descent:')
print('%f %f' % (theta[0], theta[1]))
#print('theta:', theta.ravel())
plot_linear_fit(X, theta)
plt.show()
plot_visualize_cost(X, y, theta)
plt.show()