Joeyos's Blog Software Engineer

深度学习笔记

2018-06-02
Quan Zhang
机器学习  Python
 

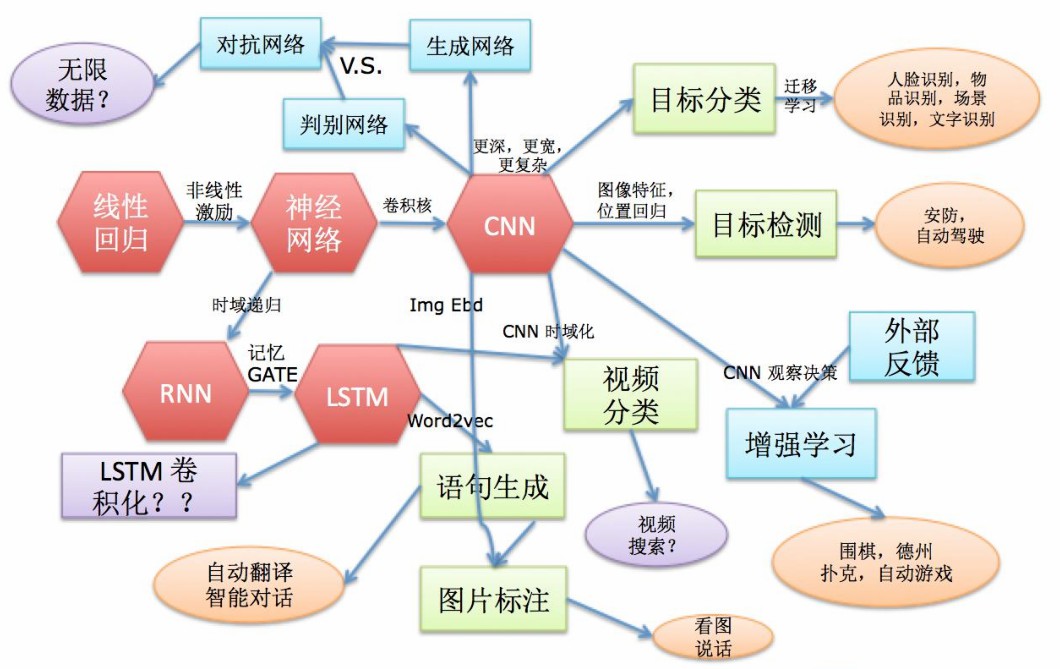
深度学习图谱

神经网络的编程基础

二分类

假如有一张图片作为输入，比如一只猫，如果识别这张图为猫，则输出标签1，否则为0。

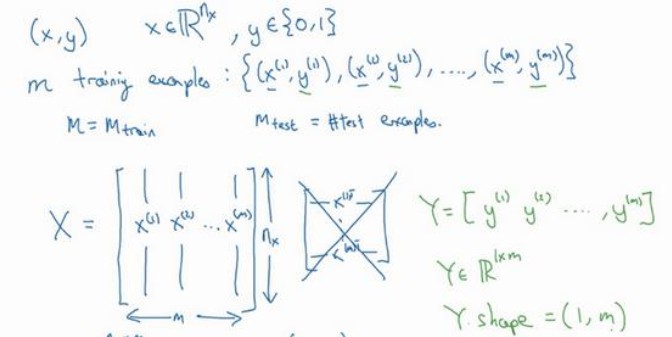
这张图片需要保存3个矩阵，对应RGB三个颜色。把这些像素值提取出来，放到一个特征向量x中，x为列向量。

符号定义：

  • $x$：表示一个$n_x$维数据，为输入数据，维度为($n_x$,1)
  • y：表示输出结果，取值0和1
  • ($x^{(i)},y^{(i)}$)：表示第$i$组数据，训练数据(默认)或者测试数据
  • $X=[x^{(1)},x^{(2)}…x^{(m)}]$：表示输入，$n_x*m$维矩阵，$m$为样本数目
  • $Y=[y^{(1)},y^{(2)}…y^{(m)}]$：表示输出，$1*m$维，一行一列

执行X.shape，则输出($n_x,m$)，Y.shape，则输出($1,m$)。

向量化

向量化可以避免使用for循环，可以加速程序运行：$z=np.dot(w,x)+b$。for循环执行时间可能比向量化慢300倍。

激活函数

  1. sigmoid函数$\frac{1}{1+e^{-z}}$：除了输出层是一个二分类问题基本不会用它

  2. tanh函数$\frac{e^z-e^{-z}}{e^z+e^{-z}}$：非常优秀，几乎适合所有场合

  3. Relu函数$max(0,z)$：常用的默认函数

激活函数的导数

  1. sigmoid：$d(g(z))=g(z)(1-g(z))$

  2. tanh：$d(g(z))=1-(tanh(z))^2$

  3. Relu：

\[d(g(z))=\begin{cases} & 0 \text { if } z<0\\ & 1 \text{ if } z>0\\ & ? \text { if } z=0 \end{cases}\]

用TensorFlow寻找J最小w

$J(w)=w^2-10w+25=(w-5)^2$，则J最小时，w=5

请测试你是否拥有TensorFlow的运行环境：

import numpy as np
import tensorflow as tf
hello = tf.constant("Hello Tensotflow!")
sess = tf.Session()
print(sess.run(hello))

b'Hello Tensotflow!'

寻求最小的J对应的w：

import numpy as np
import tensorflow as tf
# 定义参数w
w = tf.Variable(0,dtype = tf.float32)
# 定义损失函数
cost = tf.add(tf.add(w**2,tf.multiply(-10.,w)),25)
# 用0.01的学习率，目标是最小化损失
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
init = tf.global_variables_initializer()
session = tf.Session()
# 初始化全局变量
session.run(init)
print(session.run(w))# 输出为0
session.run(train)
print(session.run(w))# 输出约为0.1
# 执行1000次迭代，输出约为4.9999，接近J最小时w=5
for i in range(1000):
    session.run(train)
print(session.run(w))

0.0
0.099999994
4.9999886

其实TensorFlow冲在了一般的加减法运算，可以把cost写成更直接的形式：

# cost = tf.add(tf.add(w**2,tf.multiply(-10.,w)),25)
cost = w**2-10*w+25

加入训练集数据x，取代数字1，-10，25：

  1. 定义x接入的数据： coefficients = np.array([[1.],[-10.],[25.]])

  2. 定义x： x = tf.placeholder(tf.float32,[3,1])

  3. 定义损失函数： cost = x[0][0]w**2+x[1][0]w+x[2][0]

  4. 在训练中把数据接入x： session.run(train,feed_dict={x:coefficients})

import numpy as np
import tensorflow as tf
# 定义x接入的数据
coefficients = np.array([[1.],[-10.],[25.]])
# 定义参数w
w = tf.Variable(0,dtype = tf.float32)
# 定义x
x = tf.placeholder(tf.float32,[3,1])
# 定义损失函数
# cost = tf.add(tf.add(w**2,tf.multiply(-10.,w)),25)
cost = x[0][0]*w**2+x[1][0]*w+x[2][0]
# 用0.01的学习率，目标是最小化损失
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
init = tf.global_variables_initializer()
session = tf.Session()
# 初始化全局变量
session.run(init)
print(session.run(w))# 输出为0
session.run(train,feed_dict={x:coefficients})
print(session.run(w))# 输出约为0.1
# 执行1000次迭代，输出约为4.9999，接近J最小时w=5
for i in range(1000):
    session.run(train,feed_dict={x:coefficients})
print(session.run(w))

0.0
0.099999994
4.9999886

机器学习策略

当你构建一个深度学习系统时，不知道最终结果是好是坏，或许白费几个月的时间，所以需要一些有效的方法预先判断哪些想法是靠谱的。

正交化

如同调电视机一样，不同按键对应不同功能，才能达到最终的目的。搭建机器学习系统时，可以尝试和改变的东西太多，有太多的参数可以调，你要知道，对于调整什么来达到某个效果。

单一数字评估指标

无论你是调整超参数还是尝试不同的学习算法，如果你有一个单一的评估指标，你的进展会快很多。

对于分类器，一个合理的评估方式是查准率和查全率的折中表达：

$F1=\frac{2PR}{P+R}$

优化指标

准确率和时间往往是矛盾的。但可以设定一个阈值，比如在100ms内，不管时间多少，只要准确率高，时间都在接受范围内。

开发集和测试集大小

对于100个小样本，采用7/3或者6/2/2是合理的；对于100万的大样本，98/1/1已经够了。

迁移学习

在深度学习中，最强大的理念之一就是，有的时候神经网络可以从一个任务中学习，并将学得的知识应用到另一个独立的任务中。

如果你要做一个计算机视觉的应用，相比于从头训练权重，或者说从随机初始化权重开始，如果你下载别人已经训练好的网络权重，你通常能够进展的相当快，用这个作为预训练，然后转换到你感兴趣的任务上。

多任务学习

在迁移学习中，你的步骤是串行的，你从任务A里学习只是然后迁移到任务B。在多任务学习中，你是同时开始学习的，试图让单个神经网络同时做几件事情，然后希望这里每个任务都能帮到其他所有任务。

对于一幅图$x^{(i)}$，可用4个标签$y^{(i)}$：有无行人，有无车，有无信号灯，有无交通标志。然后同时寻找图中的这四个标签。

对于小数据集，用迁移学习；对于大数据集，用多任务学习。

端到端学习

省去流水线的开发流程，直接用别人的训练集，学到x和y之间的函数映射。如果你的数据集很小，传统方法表现可能很好；但如果你的数据集很大，端到端方法或许是一个好方法。

卷积神经网络

三维卷积

彩色图像如果是6x6x3，用一个3x3x3的三维卷积核来卷积，最后的输出为4x4x1的图像：

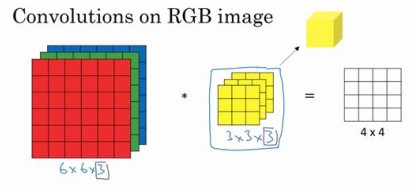
实际上就是计算一个3x3x3立方体三个分层的卷积和，可以把绿色和蓝色层卷积核设置为0，单独交算红色。

池化层

除了卷积层，卷积网络也经常使用池化层来缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性。

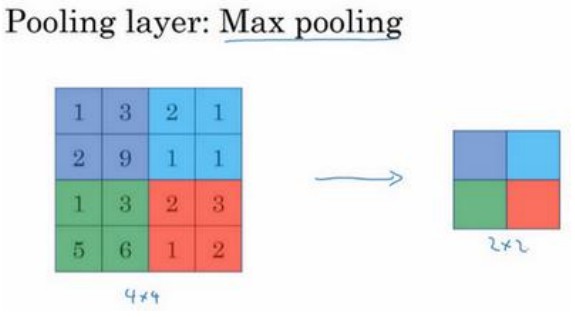
最大池化

假如输入为4x4矩阵，用到的池化类型为最大池化，树池是2x2矩阵，输出的元素为对应区域的最大值：

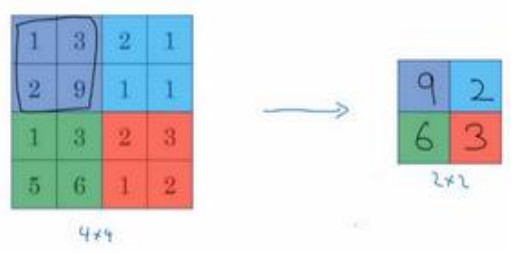
平均池化

所谓平均池化，就是取每个区域的平均值，但不常用。

残差网络

非常非常深的神经网络时很难训练的，因为存在梯度消失和梯度爆炸的问题。 跳跃连接 ，它可以从某一层网络层获取激活，然后迅速反馈给另外一层，甚至是神经网络的更深层。我们可以利用跳跃连接构建能够训练深度网络的ResNets（残差网络），有时深度能够超过100层。

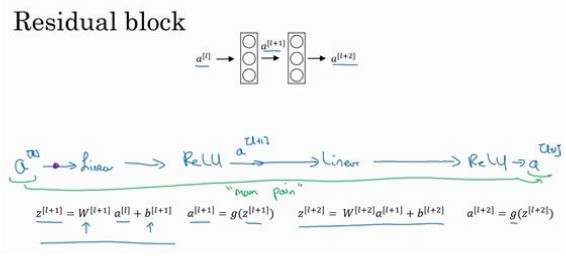
这是一个两层神经网络，在L层进行激活，得到$a^{[l+1]}$，再次进行激活，两层之后得到$a^{[l+2]}$。计算过程是从$a^{[l]}$开始，首先进行线性激活，得到$z^{[l+1]}$。然后通过ReLU非线性激活函数得到$a^{[l+1]}$。再进行线性激活，得到$z^{[l+2]}$，最后进行ReLU非线性激活，得到$a^{[l+2]}$。

对于残差网络有一点变化，其将$a^{[l]}$直接向后，传到线性激活的步骤后面，即最后的$a^{[l+2]}$的等式发生变化，加上的$a^{[l]}$产生了一个残差块。

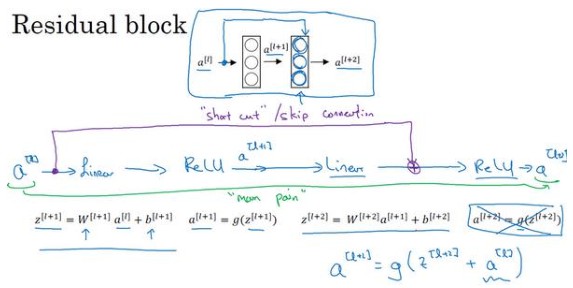
残差网络的发明者是何凯明、张翔宇、任少卿和孙剑，残差块能够训练更深的神经网络。ResNets实现地址：Github

对于普通网络，把它变成ResNet的方法是加上 跳跃连接 ，如下图，5个残差块构成一个残差网络。

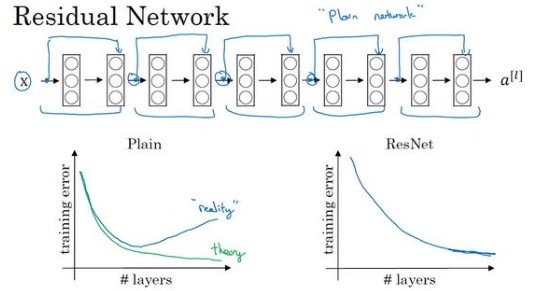
在一般的网络使用梯度下降，如果没有残差，随着深度的加深，训练错误会先减少，然后增多。而对于残差网络，就算是训练深度100层的网络也能达到很好的效果。

目标检测

卷积的滑动窗口

在图片上剪切一块区域，假设它的大小为14x14，把它输入到卷积网络。继续输入下一个区域，大小同样是14x14，重复操作，直到某个区域识别到汽车。

缺点：边界框的位置不够准确。

YOLO算法边界框预测

在滑动窗口中，你取这些离散的位置集合，然后在它们上运行分类器，在这种情况下，这些边界框没有一个能完美匹配汽车位置。也许某个框是最匹配的，但还有更确切的值，有的边界框甚至不是方形。

如何得到准确边界框？ YOLO 算法能够得到更精准的边界框。

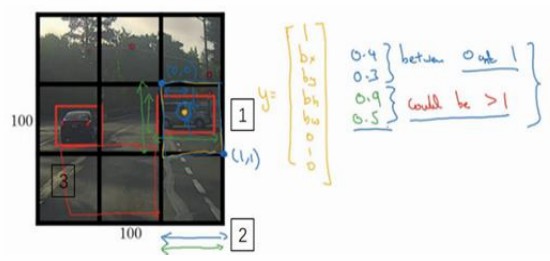
  1. 输入图像为100x100，放置一个3x3的9宫格，为精确可能是19x19的网格。

  2. 对这些小格子分别使用图像分类和定位算法。定义训练标签$y=[p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3]^T$，对于每一个格子都有这么一个向量。其中，$p_c$等于0和1取决于这个格子是否有对象。$b_x,b_y,b_h,b_w$给出边界框坐标。如第6个格子的汽车橙色中点，$b_x$大概0.4(水平)，$b_y$大概0.3，红框宽度大概为格子的0.9，高度0.5左右，所以$b_h、b_w$为0.9和0.5。$c_1,c_2,c_3$为识别的三个类别，如：行人，汽车和摩托车。

  3. 输出为3x3x8维的向量

交并比评价函数

交并比(intersection over union)可以评测目标检测算法的运作性能：

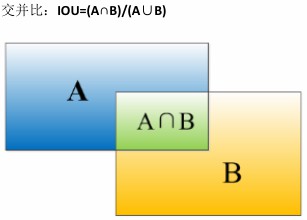
A为算法给出的边界框，B为实际的边界框，一般约定如果loU大于0.5，就算检测正确，越高越精确。

非极大值抑制

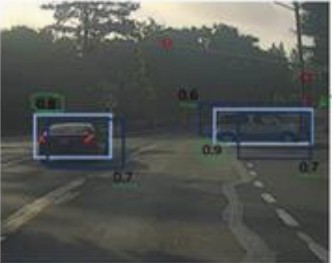
算法可能对同一对象作出多次检测，所以算法不是对某个对象检测出一次，而是检测出多次。非极大值抑制这个方法可以确保你的算法对每个对象只检测一次。

  1. 找出最高的检测概率，即右边车辆淡蓝色框0.9，然后考虑与它交并比高的边框，这些边框会被抑制、变暗，这两个矩形分别是0.6和0.7

  2. 然后找剩下的矩形，找出概率最高的0.8，即左边车辆，再抑制与其重叠的其他边界框

  3. 可以设定阈值丢掉一部分被抑制的编辑框

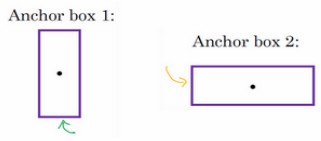
Anchor Boxes

Anchor Boxes，可以让一个格子检测出多个对象，即同时检测到人和汽车。如果选择两个box，则输出为：

\[y=[p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3,p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3]^T\]

前8个参数用于检测box1类似的目标，后8个检测跟box2类似的目标。

人脸识别

一次学习

人脸识别所面临的一个挑战就是需要解决一次学习(one-shot)问题。你需要通过仅仅一张图片当训练样本就能去识别这个人。

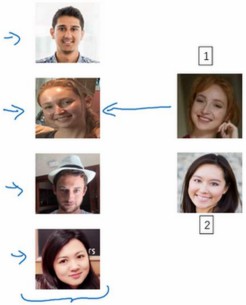
你需要学习一个Similarity函数d，d(img1,img2)小于阈值则相似，大于阈值则不相似。

Siamese网络

为了实现Similarity函数d，我们使用Siamese网络。

triplet损失

要想通过学习神经网络的参数来得到优质的人脸图片编码，方法之一就是定义三元组损失函数，然后应用梯度下降。所谓三元组，就是anchor目标图片，positive图片和negative图片，需要目标图片近似positive图片，与negative图片相差很大。

二分类

triplet损失是一个学习人脸识别卷积网络参数的好方法，还有其他学习参数的方法，让我们看看如何将人脸识别当成一个二分类问题。选课一对神经网络，选取siamese网络，同时计算这些嵌入，然后将其输入到逻辑回归单元进行预测，相似则输出1，否则为0。

循环神经网络RNN

传统的机器学习算法非常依赖于人工提取特征，使得基于传统机器学习的图像识别、语音识别以及自然语言处理等问题存在特征提取的瓶颈。基于全连接神经网络的方法也存在参数太多、无法利用时间序列信息等问题。

循环神经网络能挖掘数据中的时序信息以及语义信息的深度表达能力，循环神经网络RNN模型在语音识别、自然语言处理和其他领域中引起了变革。

循环神经网络的主要用途是处理和预测序列数据。理论上循环神经网络可以支持任意长度的序列，然而在实际中，如果序列过长会导致优化时出现梯度消散的问题，所以实际中一般会规定一个最大长度，当序列长度超过规定长度之后会对序列进行截断。

前向传播

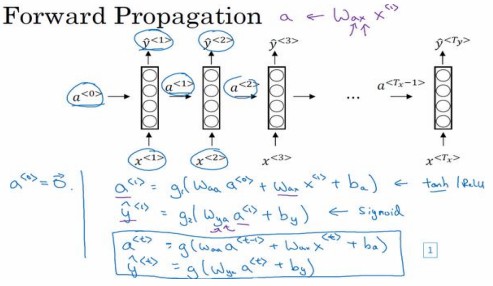
一般开始先输入$a^{<0>}$，它是一个零向量，接着就是前向传播过程，先计算激活值$a^{<1>}$，然后再计算$y^{<1>}$。

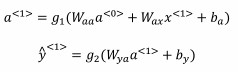
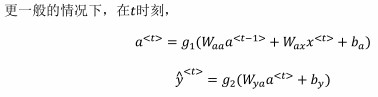
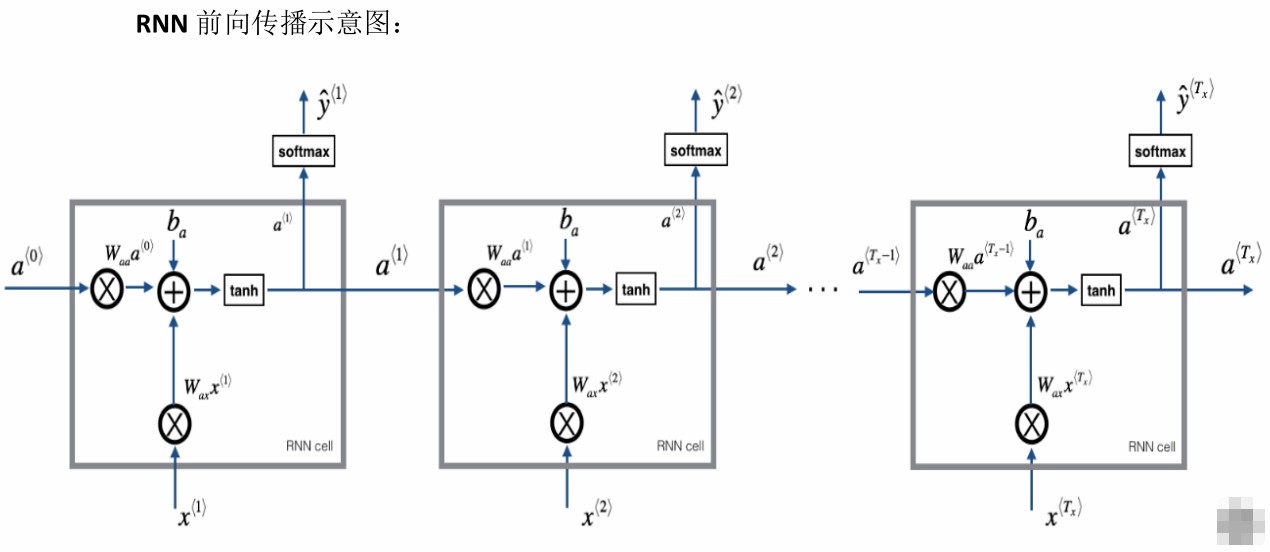
一般循环神经网络的激活函数为$g_1$为tanh。对于二分类，可以用sigmoid；对于k分类，可以用softmax。

反向传播

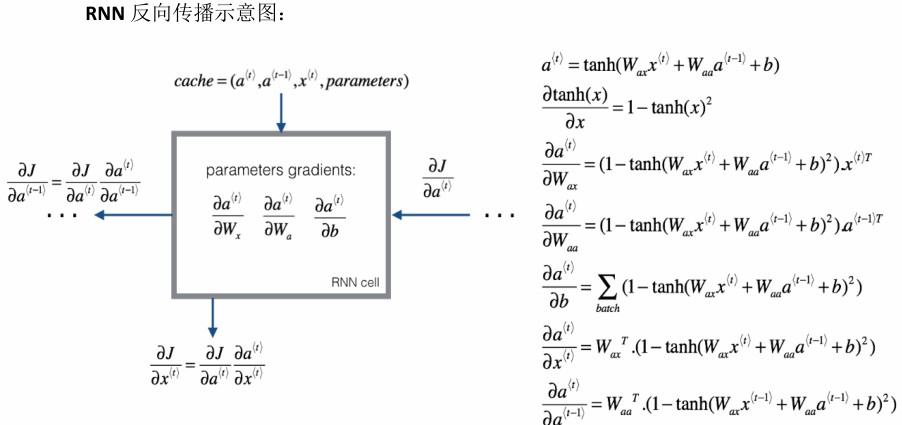
梯度消失

随着神经网络层数的增加，导致有可能指数型的下降或增加，我们可能会遇到梯度消失或者梯度爆炸的问题。对于梯度爆炸可以采用梯度修剪来解决，对于梯度消失，可以采用GRU（门控循环单元网络）。

GRU单元

门控循环单元，它改变了RNN的隐藏层，使其可以很好地捕捉深层链接，并改善梯度消失的问题。

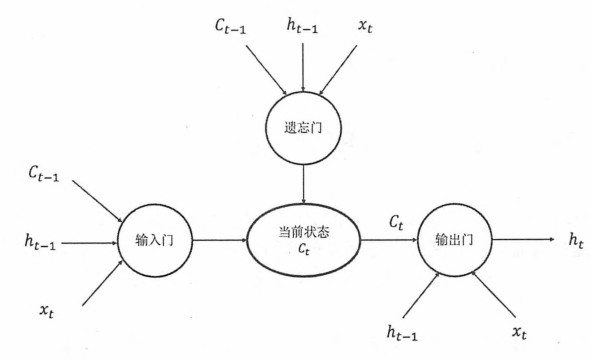
LSTM长短期记忆

GRU门控循环单元能够让你可以在序列中学习非常深的连接，但LSTM长短期记忆更有效。

循环神经网络工作的关键点是使用历史的信息来帮助当前的决策。有的模型仅仅需要短期的上下文信息足矣，有些模型需要较远的上下文信息才能预测待预测的信息。与单一tanh循环体结构不同，LSTM是一种拥有三个门结构的特殊网络结构。遗忘门会根据当前输入$x_t$、上一时刻状态$c_{t-l}$和上一时刻输出$h_{t-l}$共同决定哪一部分记忆需要被遗忘。同样输入门根据门结构决定哪部分输入补充新的记忆。

双向循环神经网络BRNN

双向RNN模型不仅可以获取某点之前的信息还可以获取未来的信息。

强化学习

经过短期的激励方程，长期的价值方程，用于指导训练。通过训练，学到最优的映射关系。常见的有DQN深度增强学习模型和A3C模型。

Similar Posts

上一篇 机器学习笔记

下一篇 用Sheffield遗传工具箱求最优值

Comments

Content